Introduction
Is it possible to safely reduce the number of SCRAM password hashing iterations from 4096 to just one?
An engineer recently raised this question about our password generation to optimise CPU usage. Why? In Neon, every database is secured via a password. Verifying the password takes a certain amount of compute every time a connection is established. We want to make connections as fast as possible.

In the world of cybersecurity, even minor adjustments can raise significant questions and debate; this doesn’t appear to be a minor adjustment. Our debate centered around these questions:
- Can we compensate for this by adjusting the password length?
- With the aim of optimising CPU usage and minimising latency, we confront a critical dilemma: how to maintain balance between security and resources while improving performance?
The Debate: Security Considerations
When we consider security best practices, OWASP recommends PBKDF2 (which we use as part of the SCRAM protocol) with 600,000 rounds. So, how can we even discuss reducing the hash iteration count to 1? Although 4k is considered low nowadays, the impact of hashing 4k is measurable, but what about 1? Is it unlikely for an attacker to possess sufficient CPU support for a successful brute-force attack? If we decrease the password hash iteration count from 4096 to 1, can we expect to gain 4096 times the entropy to fully compensate for security?
The answer is that the iterations make the hash more expensive to calculate, which slows down a dictionary attack. But at Neon we generate the passwords randomly. Therefore a dictionary attack here is not feasible. Although a brute-force attack is still possible, we can make it more expensive by simply making the password longer.
Let’s put these questions into perspective with some numerical analysis. Take a look at the code snippet below, responsible for generating database passwords:
func GenerateNewPasswordForRole() (secret.String, error) {
pwd, err := password.Generate(12, 2, 0, false, false)
if err != nil {
return secret.String{}, fmt.Errorf("cannot generate password: %w", err)
}
return secret.NewString(pwd), nil
}Calculating Entropy
To calculate the entropy, we employ the following formula, determining the brute-force strength in terms of the number of SHA computations required to try all possible passwords:
Brute-force strength = password-entropy + log2(PBKDF2 iterations)
Here’s how we break it down:
- Brute-force strength indicates how resistant the password is to brute-force attacks, expressed as the number of SHA computations needed.
- Password-entropy represents the entropy of the password in bits.
- PBKDF2 iterations is the number of iterations used in the PBKDF2 key derivation function.
The function password.Generate() creates a random password based on specified parameters like length, number of digits, symbols, uppercase letters, and whether character repetition is allowed.
For example, password.Generate(12, 2, 0, false, false) generates a 12-character password with at least 2 digits, no symbols, no uppercase letters, and no repeated characters.
Considering these parameters, we can assess the number of possible combinations for various values:
Brute Force Strength
| Title | PW length (characters) | PW entropy (bits) | PBKDF2 iterations | Brute-force strength |
| current | 12 | 68.20834109 | 4096 | 80.20834109 |
| allow repetitions | 12 | 71.45035572 | 4096 | 83.45035572 |
| allow repetitions, reduced iterations | 12 | 71.45035572 | 1 | 71.45035572 |
| some reduced iterations | 12 | 71.45035572 | 512 | 80.45035572 |
| some more reduced iterations | 13 | 77.40455204 | 8 | 80.40455204 |
| longer pw, reduced iterations | 14 | 83.35874835 | 1 | 83.35874835 |
| goal: 128bit | 20 | 119.0839262 | 4096 | 131.0839262 |
| goal: 128bit, reduced iterations | 22 | 130.9923188 | 1 | 130.9923188 |
| goal: 256bit | 41 | 244.1220487 | 4096 | 256.1220487 |
| goal: 256bit, reduced iterations | 43 | 256.0304413 | 1 | 256.0304413 |
If you look at the above table, increasing the password length by 1 nearly compensates for reducing iterations 8 times, which shows the comparison is not linear.
Alternatively, reducing iterations by 4096 times is nearly the same as increasing characters by 2 and allowing repetitions, to the maximum extent.
Password Cracking Techniques
Now, turning to password cracking techniques:
The SCRAM-SHA-256 algorithm generates a 256-bit ClientKey from the plaintext password using PBKDF2. Interestingly, exceeding 256 bits of password entropy doesn’t enhance security, as the derived ClientKey remains the primary target for attackers.
Consider two primary methods of password cracking: dictionary attacks and brute-forcing. While the former becomes infeasible with random passwords, brute-forcing persists as a concern, particularly when the original password lacks 256 bits of entropy, raising doubts about its viability.
Expanding the password length is a potential solution. Extending it to 43 alphanumerical characters surpasses the 256-bit ClientKey’s entropy, significantly hindering brute-forcing attempts. However, this poses challenges to user experience, as longer passwords are less convenient.
In terms of iteration counts:
With 1 iteration, an attacker needs a single SHA-256 calculation per guess. Conversely, 4096 iterations require 4096 calculations per guess. Notably, reducing iterations from 4096 to 1 has an impact equivalent to adding 12 bits to the password’s length in random generation.
In a rough estimate, adding 2 characters to the original password length provides a similar increase in brute-force resistance as the loss incurred by reducing iterations from 4096 to 1.
These assessments apply specifically to randomly generated passwords. If user-supplied passwords are used, vulnerable to dictionary attacks, these calculations lose their relevance from a security standpoint.
Conclusion
In conclusion, if we go back to the original question: Is it possible to safely reduce the number of SCRAM password hashing iterations from 4096 to just one? Is it even viable from security standpoint? The answer is yes! Due to randomly generated passwords eliminating the possibility of dictionary attacks, we can simply reduce the chances of successful brute-force attacks by making the password longer.
This change underscores Neon’s commitment to always seek the right balance between security and cost-efficiency when evaluating new solutions.
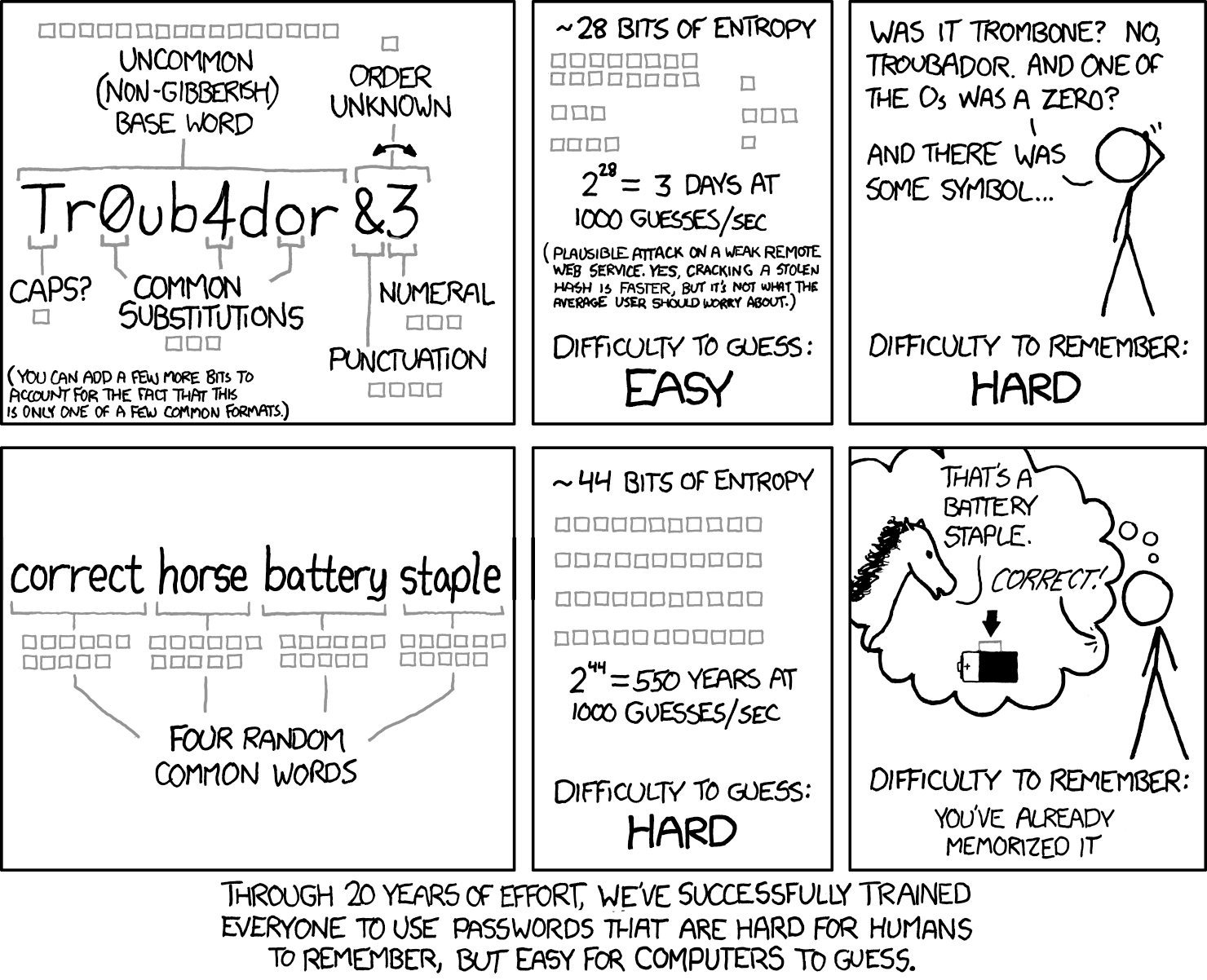
Turns out xkcd was right once again. 😉